【院試解答】東大院機械工学専攻2020流体力学
スポンサーリンク
今回は東大院機械工学専攻2020年流体力学を解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
問題を解くのに必要な知識
・境界層方程式
・層流と乱流
・質量保存則
・運動量の法則
解答本文
境界層に関しての問題です。やることが多くてかなりハードですが序盤は境界層方程式やそこまで難しくない運動量の法則なので得点したいところです。この辺は覚えるくらい繰り返しましょう。境界層は割と頻出分野で今後も出題されると思うので解けるようにしっかり対策しましょう。
(1)各項のオーダーを評価する問題
連続の式およびナビエ・ストークス方程式をそれぞれ
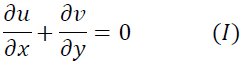
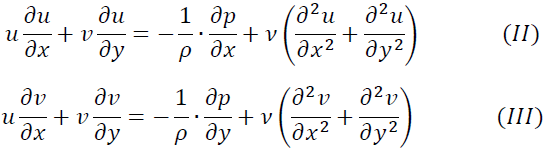
とします。式(I)の各項のオーダーは
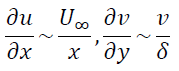
ここで、この項のオーダー同士は同程度でなければならないのでvのオーダーは
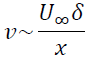
となります。よって連続の式の項のオーダーは両方とも
![]()
次に式(II)の各項のオーダーを考えていきます。まず、慣性項のオーダーを考えると
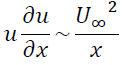
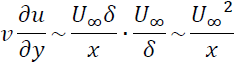
粘性項のオーダーは
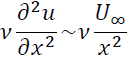
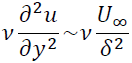
最後に式(III)について考えます。慣性項のオーダーを考えると
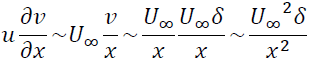
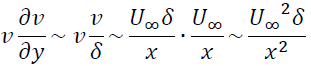
粘性項のオーダーは
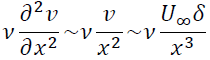
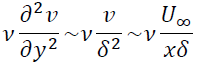
(2)境界層方程式を導出する問題
境界層方程式を導出する問題です。下の記事の東大院のH24-Iにもほぼ同じ出題があります。流れは決まってるので繰り返してできるようにしておきましょう。
それでは、ここから解答です。まず、式(III)について考えます。(1)より式(II)の各項のオーダーは
![]()
程度であるとわかります。
![]()
から式(III)の中で寄与を考慮すべき項は右辺第1項の圧力項のみであることがわかるので式(III)は
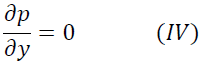
となり、境界層内ではy軸方向の圧力勾配がないことがわかります。次に式(I)は(1)で求めたオーダーより
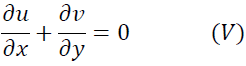
となって、式(I)と変わりません。次に
![]()
より
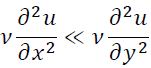
が成立するので
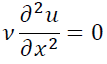
と近似できます。よって式(II)は
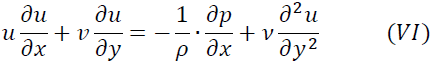
となります。次に圧力項について考えます。主流速度をUとすると境界層の境界付近ではuは主流速度Uに近付くのでy方向の変化はありません。つまり
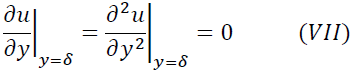
が成立します。さらに式(IV)より境界層内ではy軸方向の圧力勾配はないため、境界層内の圧力勾配と境界層の境界における圧力勾配は等しくなることがわかります。よって
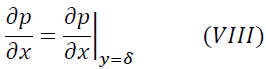
式(VI)、式(VII)、式(VIII)を考慮して境界層方程式を境界層の境界の主流に適用すると
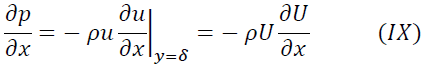
が成立します。本問では主流速度Uは常にU∞でx方向によって変更しないので式(VI)は
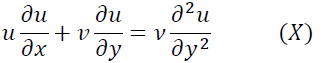
となって題意の境界層方程式を示すことができました。
(3)壁面近傍の流速分布が1次関数になることを示す問題
層流なので
![]()
これと壁面近傍では流体は粘性の影響を強く受けることから式(X)において考慮するのは粘性項のみでよく壁面近傍では式(X)は
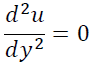
となります。この両辺をC1、C2を積分定数として積分していくと
![]()
よって壁面近傍では速度uは壁面からの距離yの1次関数となることがわかります。
(4)δとxの間に成立する関係を求める問題
式(X)より慣性力と粘性力の作用が同程度であることと(1)のオーダーより
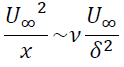
なので境界層厚さδは
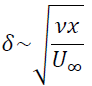
と見積もれます。
(5)層流と乱流を比較する問題
乱流による境界層では流体内の乱流運動により運動量の交換が層流と比較して活発に行われるため乱流になった場合、境界層厚さはより大きくなります。
(6)検査体積から流出する質量を排除厚さを用いて表す問題
面ADから検査体積に流入する質量流量m1は
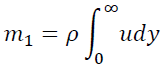
面BCから流出する質量流量m2はdxが微小であることから
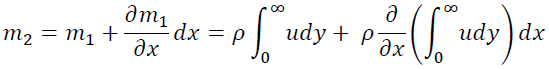
質量保存則より
![]()
が成立するのでmDCは
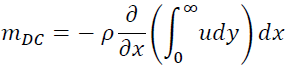
ここで排除厚さの定義より
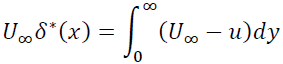
が成立するので
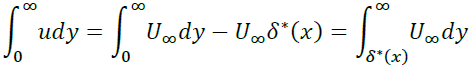
となります。以上よりmDCは
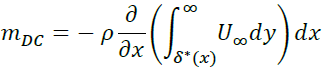
(7)壁面せん断応力を運動量厚さを用いて表す問題
これは典型問題ですね。下の記事の東大院の問題でも出題されているので絶対できるようにしておくべき問題です。でたらラッキーと思えるように練習しましょう。
それでは、ここから解答です。面ADから検査体積に流入する運動量M1は
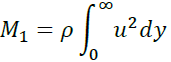
面BCから流出する運動量M2はdxが微小であることから
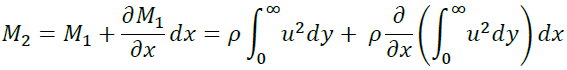
mDCは速度U∞の水平方向速度成分を持って流入するので、x方向の運動量の法則は圧力勾配がないことに注意すると
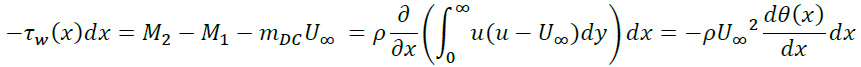
が成立します。これよりτw(x)は
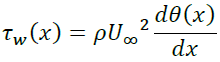

(8)質量保存則を用いる問題
下図のような破線に囲まれた検査体積を考えます。

壁面からの吸い込みや吐き出しはないため質量保存則より
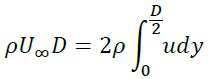
が成立します。ここで排除厚さδ*(x)の定義から
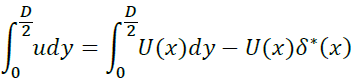
なのでこれらより質量保存則は
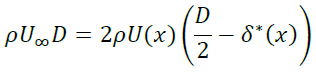
と書けます。よって主流速度U(x)は
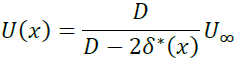
となります。
(9)圧力P(x)を求める問題
式(IX)は
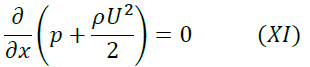
と変形できます。この両辺を積分すれば
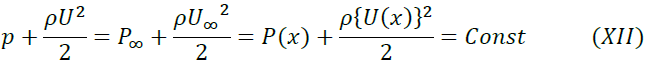
が成立します。これはおなじみのベルヌーイの定理ですね。これをP(x)について解けば
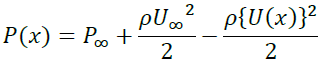
これに(8)のU(x)を代入すればP(x)は
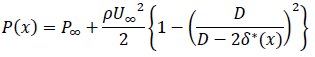
(10)壁面せん断応力を運動量厚さを用いて表す問題
運動量の法則を考える前に運動量や圧力について先に計算しておきましょう。検査体積に面ADから流入する質量流量M(x)は運動量厚さθ(x)の物理的意味から
![]()
次に面BCから流出する質量流量M(x+dx)はdxが微小であることから
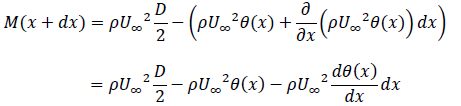
次に圧力について考えます。面BCに働く圧力P(x+dx)はdxが微小であることから
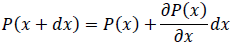
となります。これに(9)で求めたP(x)を代入すると
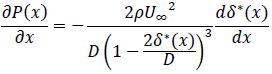
となるので、結局P(x+dx)は
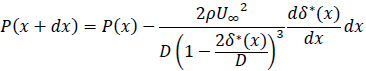
と求まります。
次に運動量の法則を考えます。面ABは壁面かつ吸い込みや湧き出しがないので、当然流入・流出する運動量はありません。次に面DCについて考えると流れの対称性からこちらからも流入・流出する運動量はないことがわかります。よって運動量の法則は右向きを正とすると
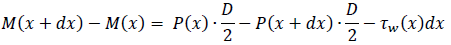
となります。これに既に計算しておいたM(x+dx)やP(x+dx)を代入すればτw(x)は
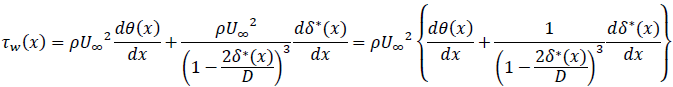
と求まります。
いやーなかなか計算が重かったですね。
やることも多くて大変な問題ですが、境界層の問題は割とパターンは決まっているので確実に得点できるようにしておきましょう。

以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |