平板層流熱伝達の問題の解答

↓の記事の解答です。

(1)各項のオーダーを評価する問題

連続の式およびナビエ・ストークス方程式をそれぞれ

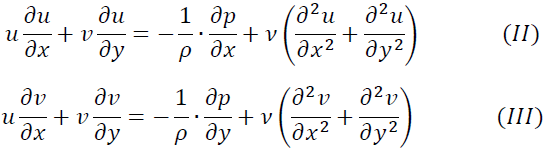
とします。式(I)の各項のオーダーは

ここで、この項のオーダー同士は同程度でなければならないのでvのオーダーは

となります。よって連続の式の項のオーダーは両方とも

次に式(II)の各項のオーダーを考えていきます。まず、慣性項のオーダーを考えると

粘性項のオーダーは

最後に式(III)について考えます。慣性項のオーダーを考えると

粘性項のオーダーは

(2)境界層方程式を導出する問題

まず、式(III)について考えます。(1)より式(II)の各項のオーダーは

程度であるとわかります。

から式(III)の中で寄与を考慮すべき項は右辺第1項の圧力項のみであることがわかるので式(III)は

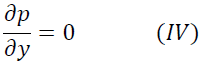
となり、境界層内ではy軸方向の圧力勾配がないことがわかります。次に式(I)は(1)で求めたオーダーより

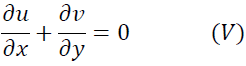
となって、式(I)と変わりません。次に

より

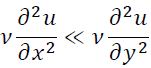
が成立するので

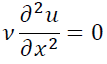
と近似できます。よって式(II)は

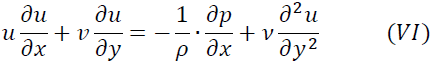
となります。次に圧力項について考えます。主流速度をUとすると境界層の境界付近ではuは主流速度Uに近付くのでy方向の変化はありません。つまり

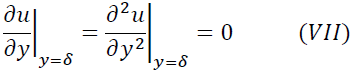
が成立します。さらに式(IV)より境界層内ではy軸方向の圧力勾配はないため、境界層内の圧力勾配と境界層の境界における圧力勾配は等しくなることがわかります。よって

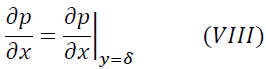
式(VI)、式(VII)、式(VIII)を考慮して境界層方程式を境界層の境界の主流に適用すると

が成立します。本問では主流速度は常にU∞でx方向によって変更しないので式(VI)は

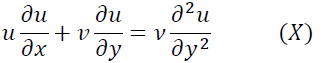
となって題意の境界層方程式を示すことができました。

(3)境界層内の速度分布を求める問題

壁面での境界条件はまず

壁面ではu=v=0なので式(X)より

次に速度境界層の外縁において考えると

ここで

なので4つの境界条件を適用して定数を求めると

となります。これより境界層内の速度分布uは

と求まります。

(4)壁面せん断応力がみたす微分方程式を求める問題

まず、検査体積における質量保存則を考えます。面ADから検査体積に流入する質量流量m1は

面BCから流出する質量流量m2はdxが微小であることから

質量保存則より面DCから流入する質量流量をmDCとすると

が成立するのでmDCは

次に検査体積内に出入りする運動量を考えます。面ADから検査体積に流入する運動量M1は

面BCから流出する運動量M2はdxが微小であることから

mDCは速度U∞の水平方向速度成分を持って流入するので、x方向の運動量の法則は圧力

勾配がないことに注意すると

となります。これよりせん断応力τw (x)がみたす微分方程式は

と求められます。

(5)速度境界層厚さδを求める問題

設問(3)で求めた速度分布を用いてθを計算すると

なので式(XⅡ)の右辺は

左辺はニュートンの粘性法則から

なので式(XⅢ)および式(XIV)から式(XⅡ)は

この両辺を積分定数をC9として積分すると

境界条件x=0でδ=0よりC9=0なので

これよりδは

(6)境界層流れのエネルギー方程式を導出する問題

エネルギー方程式を式(XⅧ)とします。

式(Ⅴ)の連続の式を用いると

式(XIX)の右辺の項のオーダーは

となります。これとδ≪Lより

なので

と近似ができる。よって式(XIX)は

と変形できます。

(7)温度境界層内の温度分布を求める問題

温度分布は

ただし、ここで

と置きました。壁面での境界条件は

壁面ではu=v=0なので式(XX)より

速度境界層の外縁において考えると

ここで

なのでこれらを適用して定数を求めると

となります。これより境界層内の温度分布は

と求まります。

(8)境界層厚さの比ξがみたす微分方程式を求める問題

面ADから検査体積に流入するエネルギーE1は比熱をcpとすると

面BCから流出するエネルギーE2はdxが微小であることから

壁面から受ける熱量qは

mDCは温度T∞で検査体積に流入するので、エネルギー収支の式は

これより

が成立します。ここで

なので式(XXⅡ)の左辺の積分は

　

次に

よって式(XXⅡ)は

ξ<1なのでξ^4の項は無視すると

ここで

なので

これをさらに変形すると

式(XV)、(XVI)よりこれは

より

とできます。ここで

なので

x0≤xなのでこれを変形して

という微分方程式が得られます。

(9)温度境界層厚さδtを求める問題

ξ^3は式(XXⅥ)を積分定数をC10として解くと

境界条件はx=x0でξ=0なのでC10は

これよりξ^3は

なのでξは

δtは

(10)局所ヌセルト数を求める問題

壁面での熱流束q'はフーリエの法則より

ニュートンの冷却法則より局所熱伝達率をhxとすると

この2式を連立するとhxは

ここで平板の加熱が平板の前縁から始まっているとき、x0=0なので式(XXⅧ)よりこのときの温度境界層の厚さδtは

なので式(XXIX)よりhxは

となります。よって局所ヌセルト数は

これより定数はそれぞれ

と求まります。

(11)平均ヌセルト数を求める問題

平均熱伝達率は

分子の積分は

なので

これから平均ヌセルト数NuLは

以上より定数はそれぞれ

と求まります。

(参考)プラントル数と境界層の厚さの比の関係

式(XXVⅡ)から平板の加熱が平板前縁から始まっているとき

なのでこれよりδ/δtは

となります。つまり

が成立するとわかります。これはH21流体、H26伝熱の記事に登場した

の関係ですね。

以上で記事は終わりです。今後も伝熱でいい感じの題材があれば記事を書こうと思います。最後まで読んでくれてありがとうございました。

人気ブログランキング

にほんブログ村