今回は東大院機械工学専攻2022年流体力学Iを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
問題を解くのに必要な知識
・連続の式
・運動量の法則
解答本文
かなり簡単な問題だと思います。できるだけ丁寧に計算してミスがないようにしましょう。特に流体内の圧力分布でP0を忘れるとかないようにしてください。僕はすぐ気が付きましたが、最初忘れてましたｗ
(1)検査面に働く力を求める問題
検査面ABに働く力は圧力によるものなので検査面ABにおける圧力分布を考えます。
下の図のように点Bを原点とし、右向き正のx軸と上向き正のy軸をとります。
そうすると検査面ABにおける圧力分布は
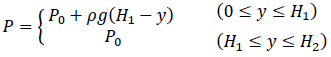
と表せます。なので力F1は
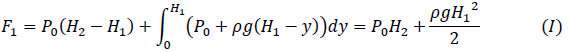
となります。
(2)検査面から流出する運動量を求める問題
検査面CDにおける流速をV2とすると連続の式から
が成立するのでV2は
これを用いるとMoutは
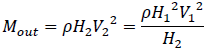
(3)運動量の法則を用いる問題
検査面ABから単位時間あたりに流入する運動量Minは
x方向の運動量の法則は壁面BCに働くせん断応力が無視できることから右向きを正とすると
となります。これからF1-F2は
と求まります。
(4)H2をg,H1,V1で表す問題
まずは問(1)と同様のやり方でF2を求めてます。検査面CDにおける圧力分布は
なので力F2は
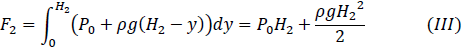
と求まります。これと式(I)からF1-F2は
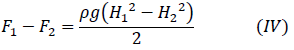
これを式(II)と連立して整理すればH2に関しての二次方程式
が得られます。これをH2>0に注意して解くと
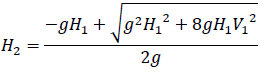
が得られます。
(5)無次元数を用いてH2<H1となる条件を示す問題
問(4)で得られたH2がH1より大きくなればいいので
という不等式が得られます。両辺とも正の数なので二乗して整理すれば
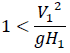
という条件式が得られます。ここでこの不等式の右辺の次元を確認してみると確かに無次元数であることがわかります。よってH1＜H2となるための条件を決定する無次元数は
であり、その条件式は
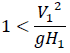
であるとわかります。
(余談)問(5)の無次元数について
問(5)の無次元数の正の平方根
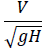
はフルード数Frという無次元数で、流体の慣性力と重力の比を表す無次元数らしいです。水理学かなんかの本読んでた時に出てきた記憶があります。興味のある方は調べてみたら面白いかもしれません。
以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |
