今回は東大院機械工学専攻2023年流体力学Iを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
問題を解くのに必要な知識
・連続の式
・運動量の法則
・等エントロピー変化
解答本文
圧縮性流体の問題ですが、検査体積まで設定してくれているので、誘導に従って解いていけばなんとかなるので頑張りましょう。この年は2題とも圧縮性流体の問題だったので戸惑った人も多かったかもしれません。こういうこともあるので今後は圧縮性流体も対策しておいた方がいいかもしれませんね。とはいえこの分野はただでさえややこしいのでそこまで高度な出題はないと個人的に思っています。最後の設問は等エントロピー変化という熱力学の知識が必要ですが、普通に対策していれば問題ないでしょう。
(1)質量保存則を用いる問題
波面とともに速度c0（右向き)で移動する検査体積（下図の赤の点線で囲まれた部分）から見ると、波面前方の気体は速度c0で検査体積に流入するように見え、波面通過後の気体は速度c0-duで検査体積から流出するように見えます。
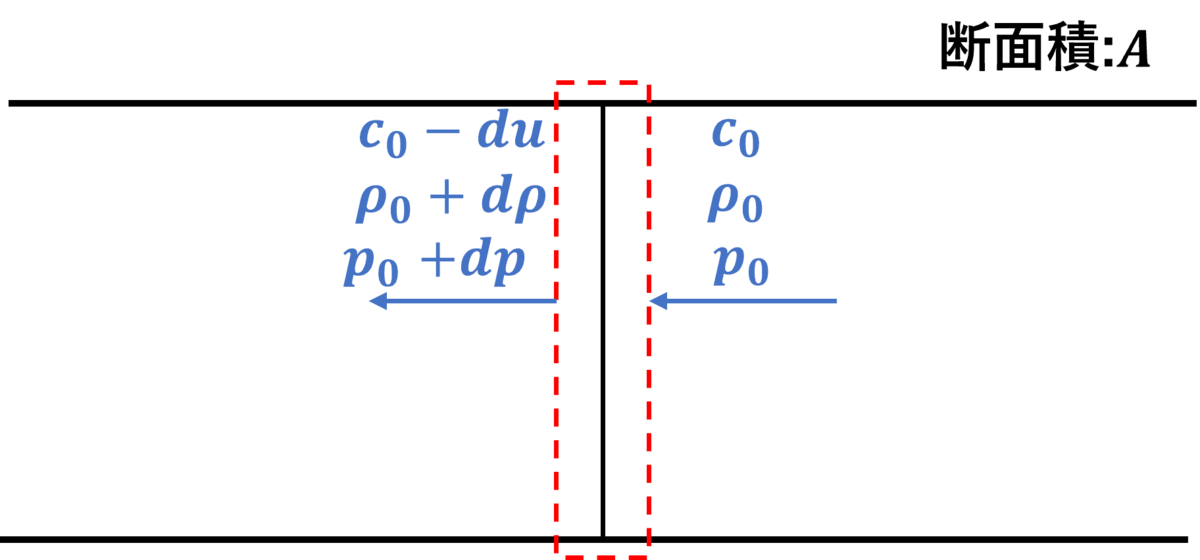
波面が通過した後の気体の密度がρ0+dρになることに注意すると質量保存則は流れに垂直な断面積をAとすると
となります。これより2次以上の微小項を無視すると
の関係が得られます。
(2)運動量保存則を用いる問題
右向きを正とすると運動量保存則は
となるので
の関係が得られます。
(3)誘起される流速の向きを答える問題
式(I)からdρ>0のときdu>0なので誘起される流速は右向き
dρ<0のときdu<0なので誘起される流速は左向き
となります。
(4)coを求める問題
式(I)および式(Ⅱ)からc0を求めると
となります。
(5)等エントロピー変化のときのcoを求める問題
熱力学第1法則より等エントロピー変化のとき
ここで理想気体の状態方程式
の両辺を微分すると
なのでdTは
これを式(IV)に代入して整理すると
ここで比体積と密度には
の関係があるので
これを式(V)に代入して
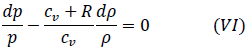
これと理想気体のマイヤーの式
および比熱比の定義
から式(VI)は
となります。よって等エントロピー変化のとき
が成立することがわかります。これと式(Ⅲ)からこの気体の状態変化が等エントロピー変化のとき、c0は
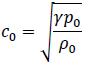
と得られます。
以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |
