今回は東大院機械工学専攻平成23年材料力学の大問Iを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
この問題を解くのに必要な知識
・片持梁のたわみ
・カスチリアノの定理 or 重ね合わせの原理と相反定理
・熱ひずみ
解答本文
(1)片持ち梁の先端のたわみを求める問題
後半の設問のことも考えて下図のように長さlの片持ち梁の左端Aからaの位置にある点Cに荷重P、右端Bに荷重Qが作用する場合を考えます。

このとき断面に生じる曲げモーメントMxをAC間(0≦x≦a)、CB間(a≦x≦l)で梁を切断して求めます。
AC間(0≦x≦a)で切断して断面より右側の部分のモーメントのつり合いを考えると


次にCB間(a≦x≦l)で切断して断面より右側の部分のモーメントのつり合いを考えると


カスチリアノの定理より点CのたわみδCおよび点BのたわみδBは


となります。ここで


なので点CのたわみδCおよび点BのたわみδBは


となります(この変形の詳細はこのページを参照)。式(2)においてPを0、Qを-Qとすればy1は

(2)片持ち梁の途中に荷重が作用している場合の問題
式(1)においてQ=0とおけばy2は

(3)B点の反力を求める問題
この時のB点のたわみをδBは式(2)においてQを-Rとすれば

となります。B点のたわみは0なので、これを0としてRを求めると

(4)C点のたわみを求める問題
式(1)においてQを-Rとして

を代入してδは

(5)C点に棒が接合された場合を考える問題
梁と棒はそれぞれ下図のように反力Rを受けます。

梁ABのC点におけるたわみyCは式(3)のPを-Rに置き換えれば得られて

となります。次に棒の変形を考えます。上で求めたyCは下向き(棒が縮む向き)を正としているので棒の変形も圧縮を正として考えます。棒の圧縮量λは反力と熱応力によって発生するので

これと式(4)の変形量が等しいとおけばRは

と求まります。 これを式(4)に代入すればyCは

と得られます。
(別解)重ね合わせの原理を用いる
(1)の最初に考えた下図のような状況におけるC点、B点のたわみ

をカスチリアノの定理を用いずに重ね合わせの原理と相反定理で求めておきます。

まず、上の問題を以下の2つの重ね合わせと考えます。
(i)C点に荷重Pのみが作用している場合

このときのC点のたわみをδC1とすると、これは長さaの片持ち梁の先端に荷重Pが生じたときの先端のたわみと等しいので

次にB点のたわみδB1を考えます。CB間には曲げが生じていないので(詳しくはこちらのページ参照)δB1は

(ii)B点に荷重Qのみが作用している場合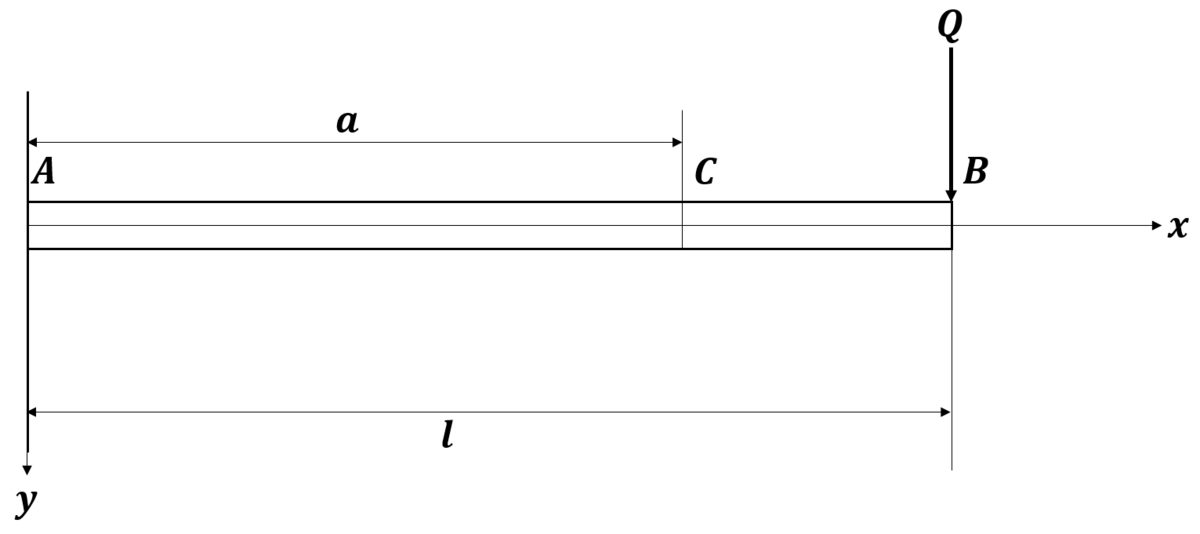
このときのC点のたわみをδC2とすると相反定理よりこれはC点に荷重Qが下向きに作用したときのB点のたわみに等しくなります。これはδB1の式のPをQに置き換えれば求まるので

次にB点のたわみをδB2とすると、これは長さlの片持ち梁の先端に荷重Qが生じたときの先端のたわみと等しいので

となります。以上(i)と(ii)の結果をそれぞれ足し合わせれば式(1)および式(2)が得られます。
以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |