今回は東大院機械工学専攻平成30年材料力学の大問IIを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
この問題を解くのに必要な知識
・梁のたわみの微分方程式(これだけでも解けます)
・カスチリアノの定理
・重ね合わせの定理
・相反定理
解答本文
片持ち梁が2本接触している問題です。完答しようと思うと計算量が結構多いので丁寧にやっていきましょう。別解では重ね合わせの原理と相反定理を使うので
を読んでおくといいです。あとは計算過程でちょくちょく
の記事内に出てくる変形を使用しているので読んだ方がわかりやすいかも。
(1)梁ACのたわみを考える問題
梁ACは図のように反力Rcを受けます。

なのでこの梁を座標xの位置で切断して断面より右側の部分でモーメントのつり合いを考えると曲げモーメントMxは

となります。

カスチリアノの定理よりたわみは

しかし、この答えではRcによって正のたわみが発生していることになっています。この問いでは下向きを正としているので符号を修正すればたわみδACは

(別解)重ね合わせの定理を用いる
重ね合わせの定理より

がすぐに求まります。
(2)梁BCDのたわみを考える問題
(4)でたわみが最大となる位置とそのたわみが問われているのでたわみ曲線の微分が必要になると考えられます。なのでたわみ曲線をたわみの微分方程式から求める方針でいきましょう。
下図のようにB点での反力をRBとします。

この梁をBC間(0≦z≦L/2)とCD間(L/2≦z≦L)で切断して曲げモーメントMzを求めます。
BC間(0≦z≦L/2)では断面より左側の部分でのモーメントのつり合いを考えるとMzは


CD間(L/2≦z≦L)も同様に断面より左側の部分でのモーメントのつり合いを考えるとMzは


これらをたわみの微分方程式

に代入して積分定数をC1、C2、C3、C4としてこれを積分していくと


ここで境界条件z=0でy=0を適用するとC3=0、z=L/2でたわみ角が連続よりC1=C2となります。これとz=L/2でたわみ曲線が連続よりC4=0となります。
z=Lは固定端なのでたわみ角0より

z=Lは固定端なのでたわみ0より

この2式よりRBとC2を求めると

となるのでたわみ角およびたわみ曲線はこれらを代入すると


これにx=L/2を代入するとδBCDは

と求まります。
(別解①)重ね合わせの原理を用いる
まず、RBを求めます。B点のたわみδBは重ね合わせの原理より
δB=(Rcによる点Bのたわみy1)+(RBによる点Bのたわみy2)
となります。ここでy2は片持ち梁の先端に集中荷重が作用したときの先端のたわみの公式からすぐに

となります。次にy1はこのページの3-1と同様に考えれば

となるのでδBは

B点は固定されているのでこれを0とすればRBは

と求まります。次にC点のたわみを考えます。梁BCDのC点のたわみδBCDは重ね合わせの原理より
δBCD=(Rcによる点Cのたわみy3)+(RBによる点Cのたわみy4)
となります。y3は長さL/2の片持ち梁の先端に荷重Rcが作用したときの先端のたわみと等しいので

となります。次にy4について考えると相反定理よりy4は点Cに荷重RBが上向きに作用したときのB点のたわみに等しくなります。(下図における点Bのたわみに等しい)

このときのB点のたわみはy1と同様に考えれば求まるのでy4は
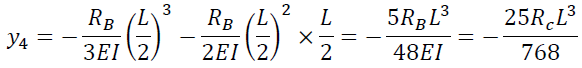
となります。よってδBCDは

(別解②)カスチリアノの定理を用いる
まずはRBを求めます。曲げモーメントMzは

なので

これとカスチリアノの定理よりB点のたわみδB(正確に言うとB点のたわみに-をかけたもの)は

となります。B点は固定されているのでこれが0とすればRBは

次にC点のたわみδBCDは

とカスチリアノの定理より

(3)反力Rcを求める問題
梁ACと梁BCDのC点のたわみが等しいので

です。式(I)と式(II)よりRcは

(4)たわみが最大になる位置とたわみを求める問題
たわみ角は

たわみyが最大になるには

となればいいのでこのときのzを求めていきます。まず

次にL/2≦z≦Lのときは

よりz=Lとなりますが両端は固定されているのでこれは不適です。なのでたわみが最大になる位置は

でこの位置でのたわみは

となります。
以上で問題は終わりです。本番では時間のことや計算量を考えて別解で(3)まで確実にやるのもいいかもしれませんね。自分の計算力とかも考慮して戦略的に得点していきましょう。
人気ブログランキング |
にほんブログ村 |