【院試解答】東大院機械工学専攻2022材料力学I
スポンサーリンク
今回は東大院機械工学専攻2022年材料力学Iを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
問題を解くのに必要な知識
・SFD
・BMD
・たわみの微分方程式
解答本文
単純支持梁の問題です。計算ミスに気を付けて解いていきましょう。
(1)梁CEのSFD、BMDを描く問題
対称性と力のつり合いから点C、E、A、Bにおける反力はすべて等しいです。この値をRとすると
![]()
となります。
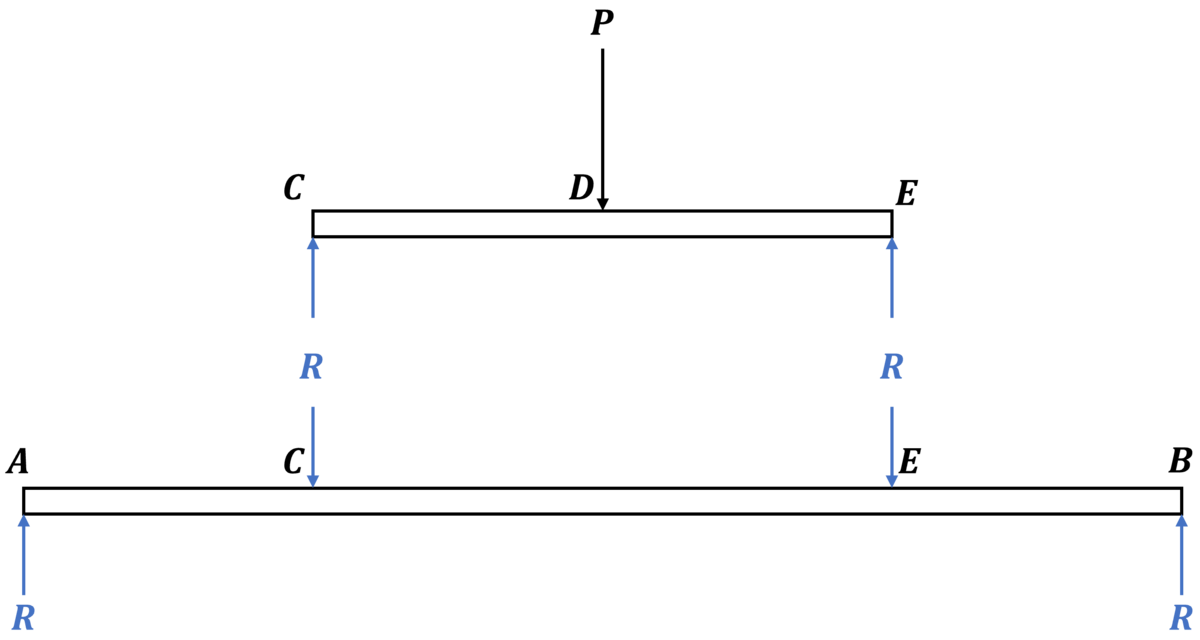
梁CEを座標xの位置で切断して力およびモーメントのつり合いを考えます。l≦x≦2lのとき、断面に生じるせん断力および曲げモーメントをそれぞれF、Mとすると断面より左側の部分における力のつり合いよりFは
![]()
モーメントのつり合いより
![]()
が成立するのでMは
![]()
となります。

2l≦x≦3lのとき、断面より右側の部分における力のつり合いよりFは
![]()
モーメントのつり合いより
![]()
が成立するのでMは
![]()
となります。

0≦x≦lおよび3l≦x≦4lのときは明らかにF、Mともに0であるからSFDおよびBMDは下図のようになります。


(2)梁ABのSFD、BMDを描く問題
梁ABを座標xの位置で切断して力およびモーメントのつり合いを考えます。0≦x≦lのとき、断面に生じるせん断力および曲げモーメントをそれぞれF、Mとすると断面より左側の部分における力のつり合いより
![]()
モーメントのつり合いより
![]()
が成立するのでMは
![]()
となります。

次にl≦x≦3lのときは断面より左側の部分における力のつりあいより
![]()
なのでFは
![]()
モーメントのつり合いより
![]()
が成立するのでMは
![]()
となります。

次に3l≦x≦4lのときは断面より右側の部分における力のつりあいより
![]()
モーメントのつり合いより
![]()
が成立するのでMは
![]()
となります。

以上より梁ABのSFDおよびBMDは下図のようになります。


(3)点Dの鉛直方向変位を求める問題
まず、梁CEについて考えます。対称性よりl≦x≦2lの部分のみを考えます。梁CEのたわみの微分方程式は
![]()
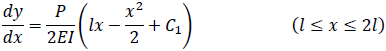

境界条件は支持端でたわみ0より
![]()
対称性から
![]()
となります。式(II)からC1は
![]()
式(I)からC2は
![]()
となるので梁CEのl≦x≦2lにおけるたわみ曲線の式は
![]()
これにx=2lを代入すると梁CEのC点を基準とする点Dのたわみy1は
![]()
次に、梁ABについて考えます。対称性より0≦x≦2lの部分のみを考えます。梁ABのたわみの微分方程式は



境界条件は支持端でたわみ0より
![]()
対称性から
![]()
となります。たわみ曲線は連続なので
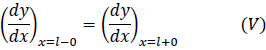
![]()
となります。式(IV)からC4は
![]()
式(III)からC5は
![]()
式(V)からC3は
![]()
式(VI)からC6は
![]()
となるので梁ABの0≦x≦2lにおけるたわみ曲線の式は

これにx=lを代入すると梁ABのA点を基準とする点Cのたわみy2は
![]()
となるので、点Dの鉛直方向変位δDは
![]()
となります。
以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |