【院試解答】東大院機械工学専攻2022材料力学II
スポンサーリンク
今回は東大院機械工学専攻2022年材料力学IIを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
問題を解くのに必要な知識
・薄肉円筒
・モールの応力円(3次元)
・ミーゼスの相当応力
・最大ひずみエネルギー説
・応力拡大係数
・破壊靭性
解答本文
題材自体は薄肉円筒ですが、第3主せん断応力を考えたり、き裂がある場合を考えたりするのであまり馴染みがない問題かもしれません。破壊力学はアホみたいに難しいのでそこまで深く問われることはないと思いますが、この問題のように破壊靭性等の破壊力学に関する知識が少し必要な設問は今後あるかもしれないので↓のような適当な教科書を軽く読んでおくといいかもしれません。
(1)軸方向応力および周方向応力を求める問題
z=lの断面で円筒を切断して、断面より下の部分で力のつり合いを考えます。
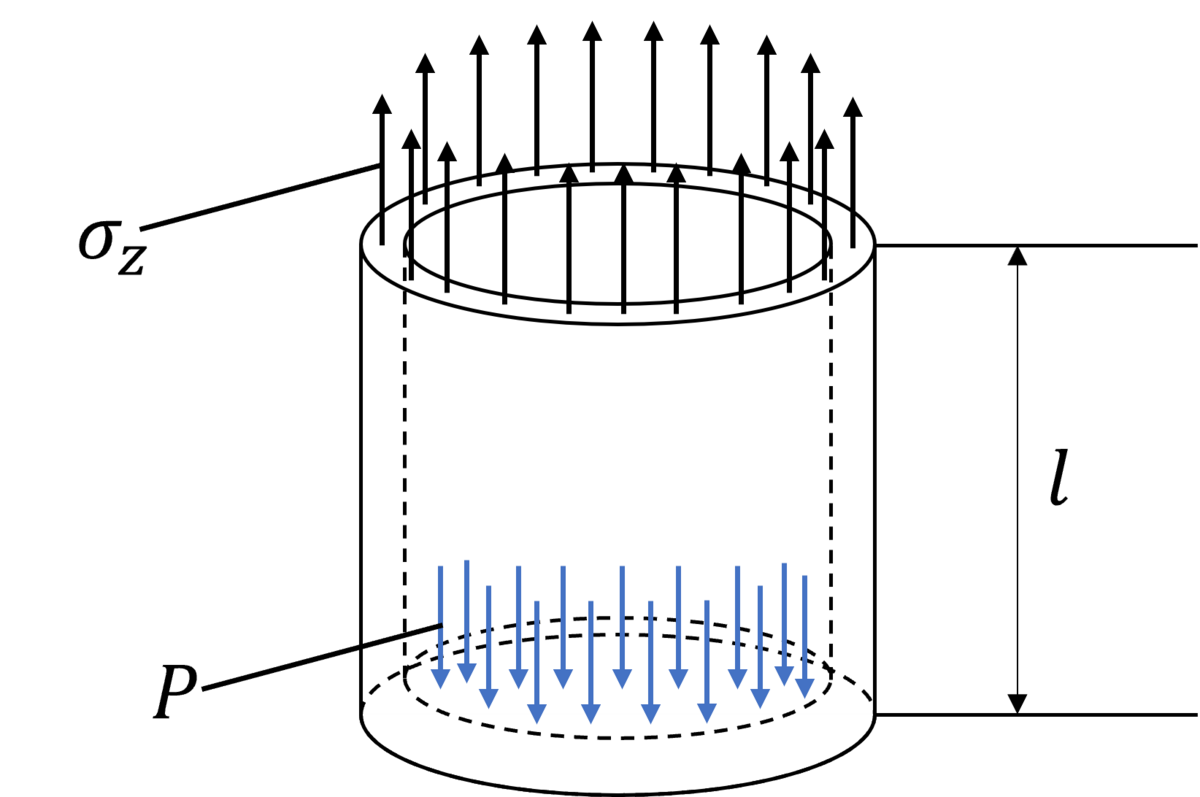
z方向の力のつり合いから
![]()
t≪rなので
![]()
よってσzは
![]()
次に上に示した長さlの円筒をさらに底面の円の中心を通り、底面に垂直な断面で切断した下図の図形を考えます。
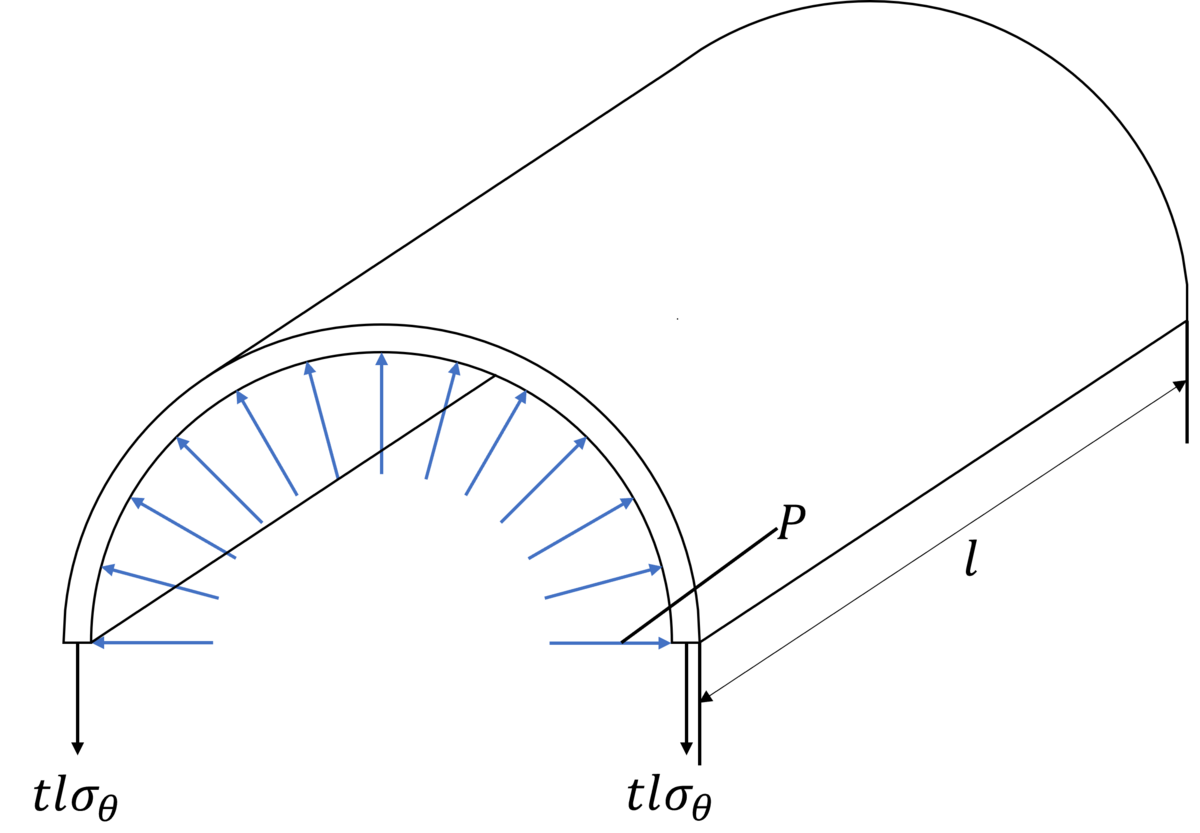
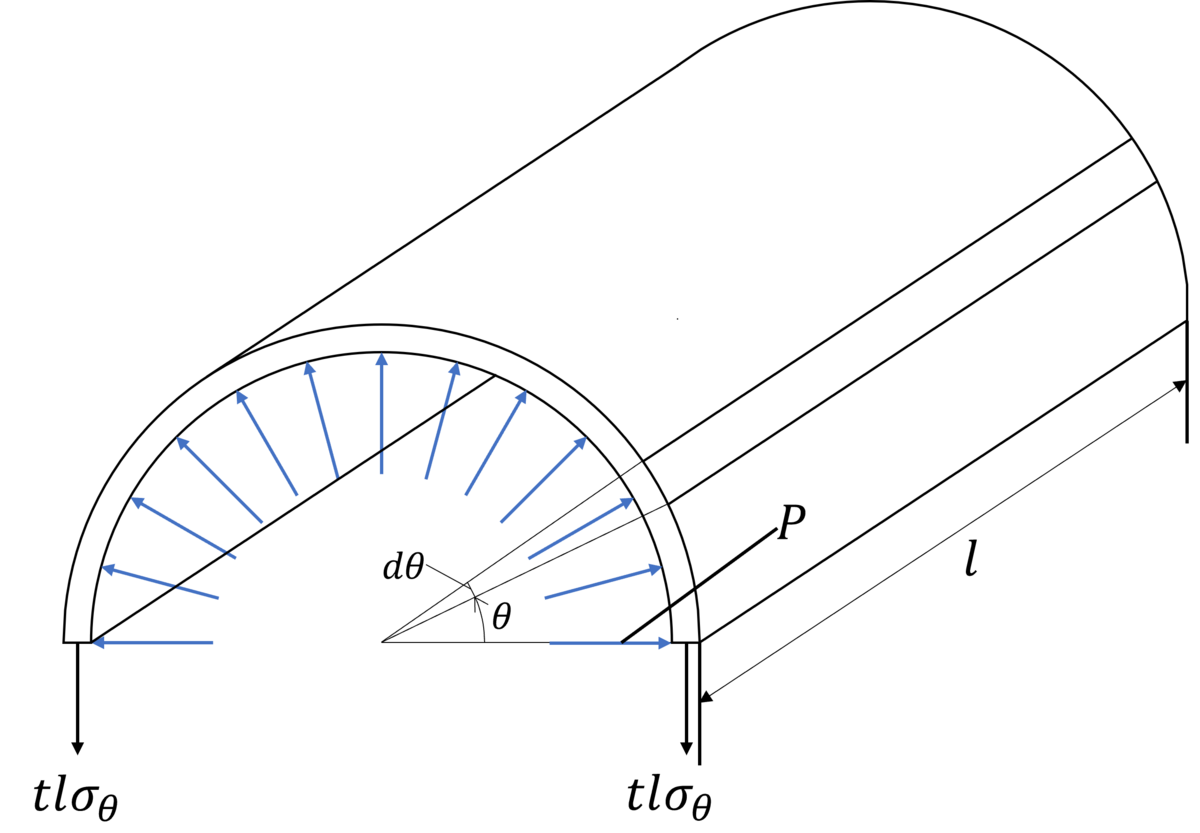
さらに下図のように微小部分dθを考えます。この微小部分に生じる内圧の周方向成分は
![]()
これをθ=0からθ=πまで積分したものと2tlσθがつりあうので
![]()
これからσθは
![]()
と求まります。
(2)主せん断応力およびミーゼス応力を求める問題
せん断応力はないので主応力σは
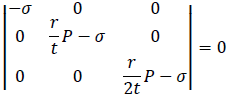
をみたします。この条件がなぜ成立するかは以下の記事を読んでください。
この条件より
![]()
が得られるので主応力σ1、σ2、σ3はそれぞれ
![]()
![]()
![]()
モールの応力円を描くと下図のようになります。
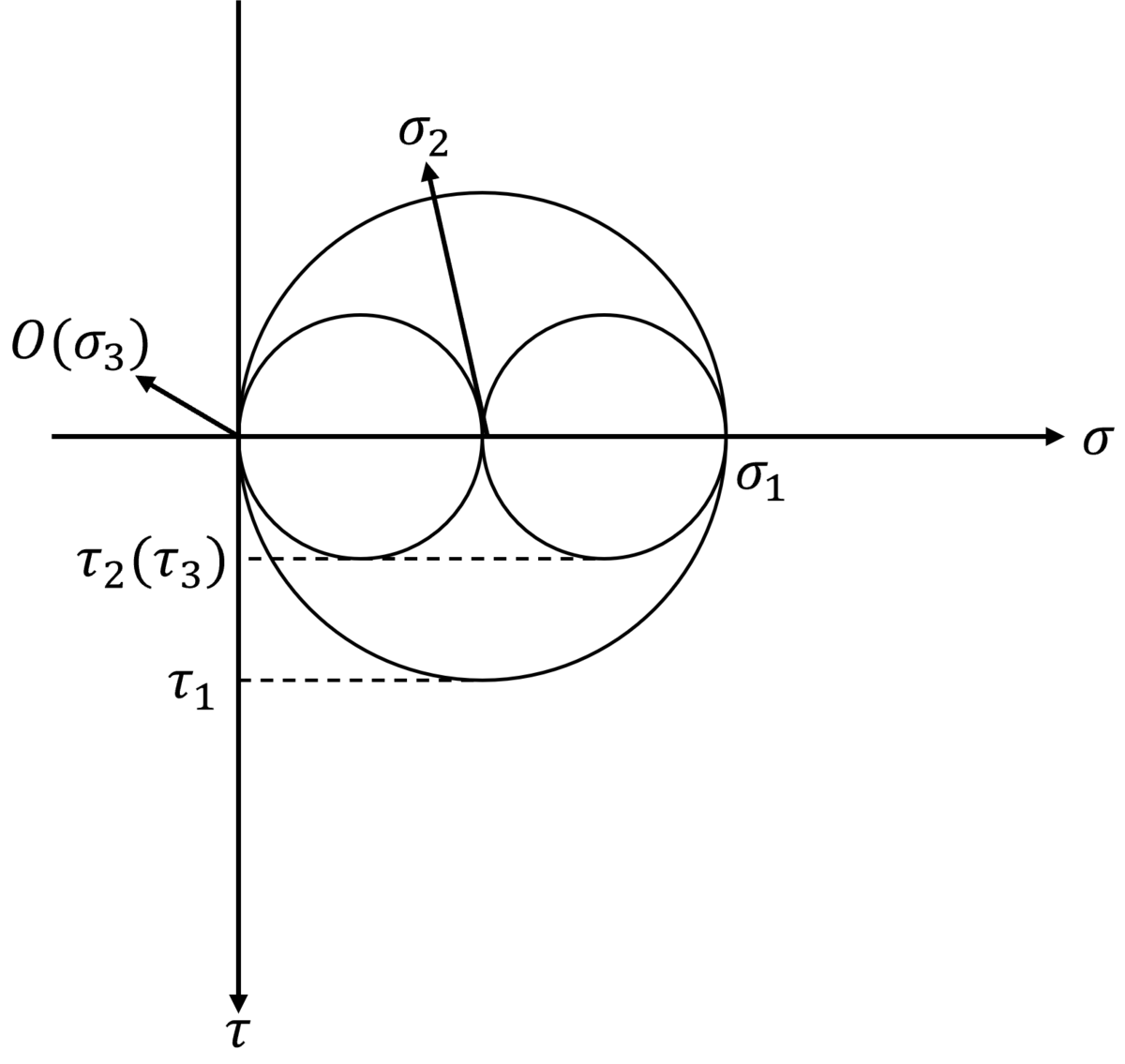
よってτ1、τ2、τ3は
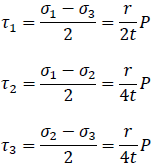
となります。次にミーゼス応力σMisesは
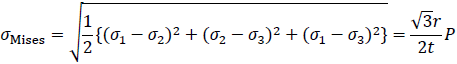
となります。
(3)塑性崩壊を生じる内圧を求める問題
最大せん断ひずみエネルギー説により、塑性崩壊が生じる条件は
![]()
これよりPfは
![]()
と求まります。
(4)き裂が進展する内圧を求める問題
き裂が進展する条件は
![]()
これよりき裂が進展を始めるとき、
![]()
が成立します。これからこのときのσθは
![]()
これと問(1)よりき裂が進展する内圧Paは
![]()
となります。
(5)Pf=Paとなるき裂長さacを求める問題
問(3)および(4)をPf=Paとなるとき
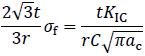
が成立するのでacは
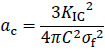
と求まります。
(6)破壊が生じる内圧とき裂長さの関係を求める問題
問(4)よりPaは
![]()
なのでaの値によって下図のように変化することがわかります。
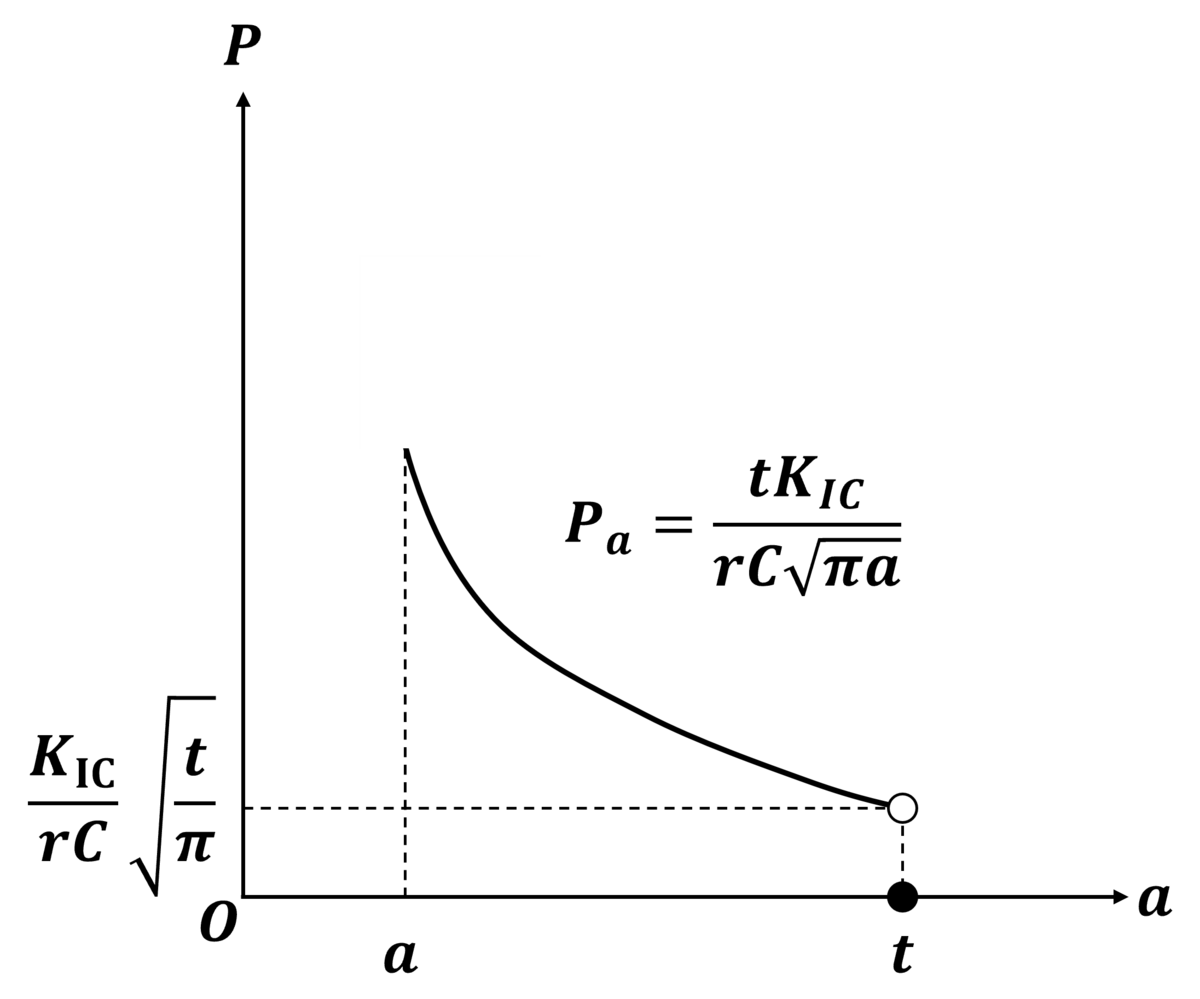
ここで、a=tのときは既にき裂が円筒内部まで進展している状態、つまり既に破壊されている状態なので破壊を生じる内圧は0となります。問(3)よりPfは定数なのでPfとPaが交わるときのaの値であるacの大きさによって破壊の様子が異なることがわかります。
なのでacの値によって場合分けして考えていきます。まず、(0<)ac<a<t、つまり
![]()
のときはPa<Pfとなるので、き裂進展による破壊が生じます。このときの内圧Pは
![]()
となります。
次にac=aのときはPa=Pfなのでき裂進展か塑性崩壊によって破壊が生じます。このときの内圧Pは
![]()
となります。
次に、0≦a<ac(<t)、つまり
![]()
のとき、Pf<Paより塑性崩壊により破壊が生じます。このときの内圧Pは
![]()
となります。またa=tのときはき裂が内部まで進展しており、既に破壊されている状態なので内圧Pは0となります。以上より
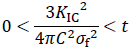
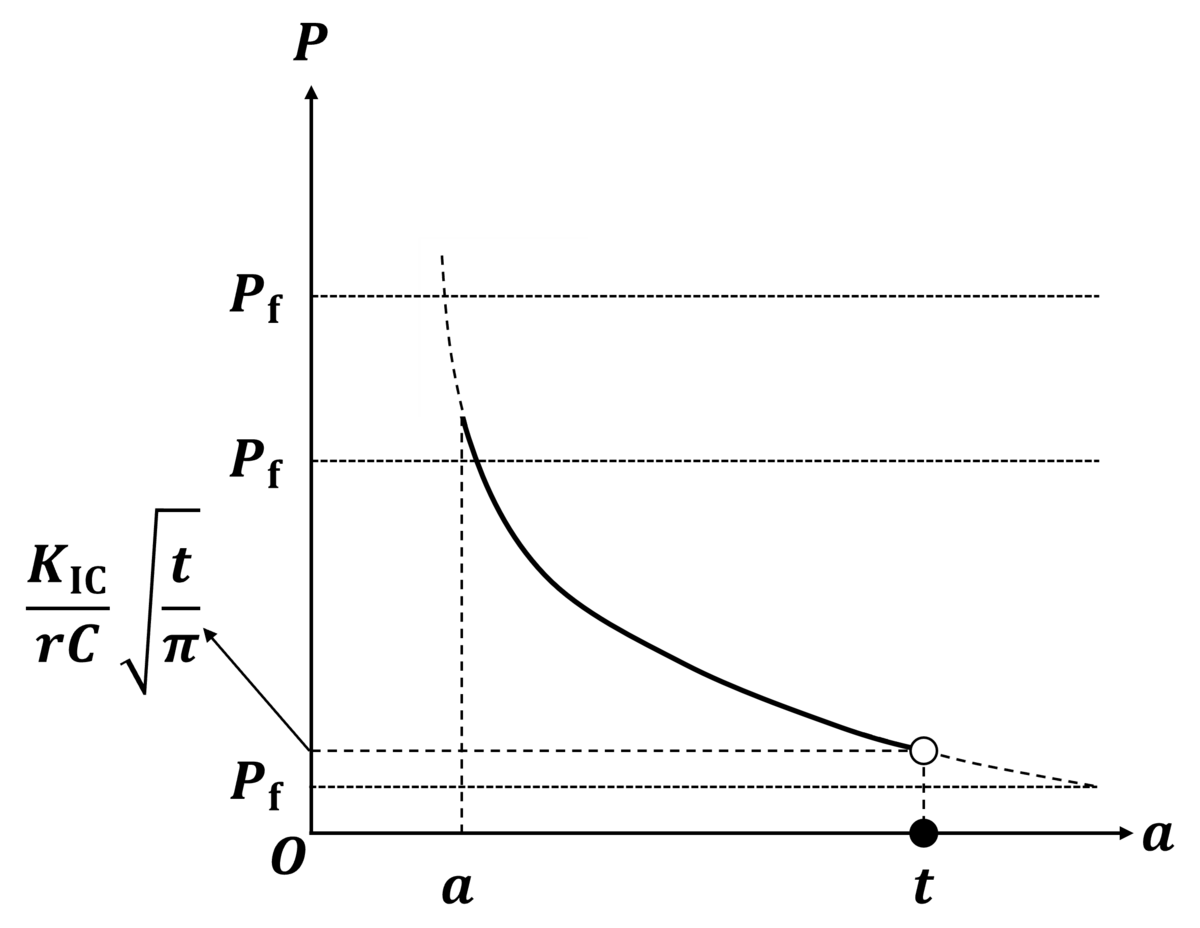
のときの破壊が生じる内圧とき裂長さaとの関係を図示すると次の図のようになります。
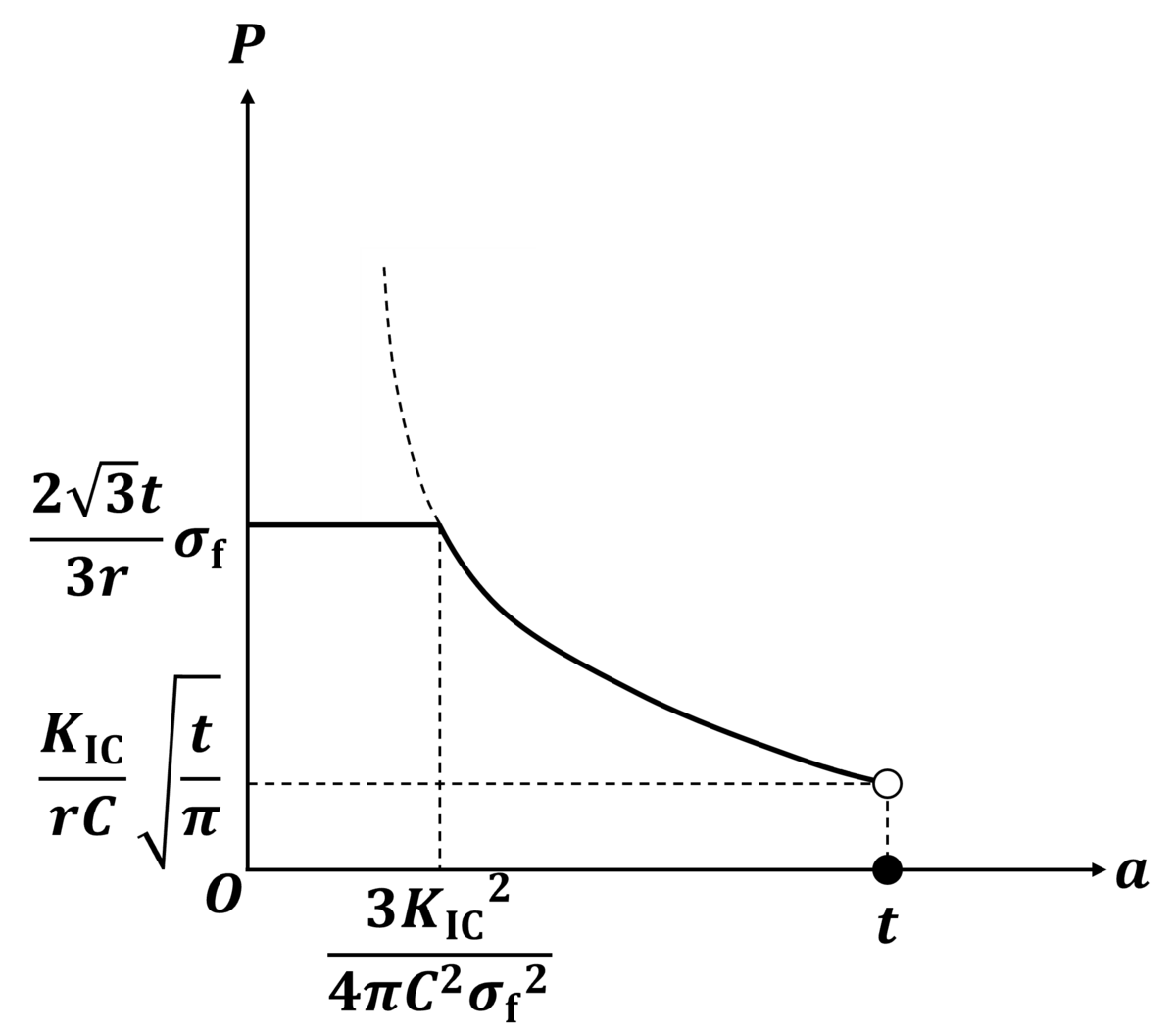
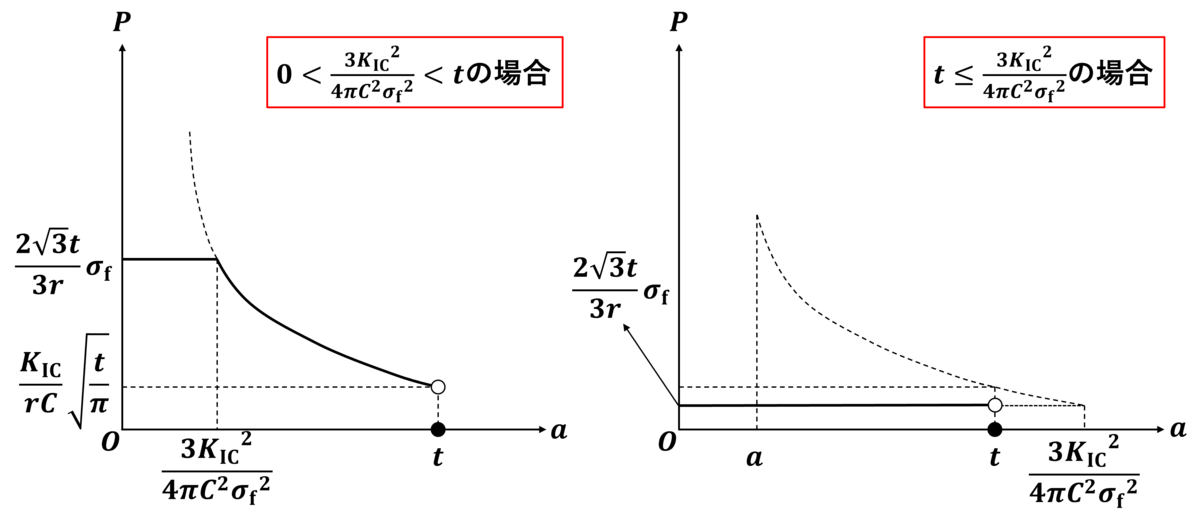
最後にt≦ac、つまり
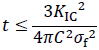
の場合を考えると、Pf≦Paよりt=acの時は塑性崩壊またはき裂進展によって、t<acのときは塑性崩壊により破壊が生じます。いずれの破壊様式のときも内圧Pはa=t以外では
![]()
となります。a=tのときはき裂が内部まで進展しており、既に破壊されている状態なので内圧Pは0となります。よって
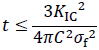
のときの破壊が生じる内圧とき裂長さaとの関係を図示すると次の図のようになります。
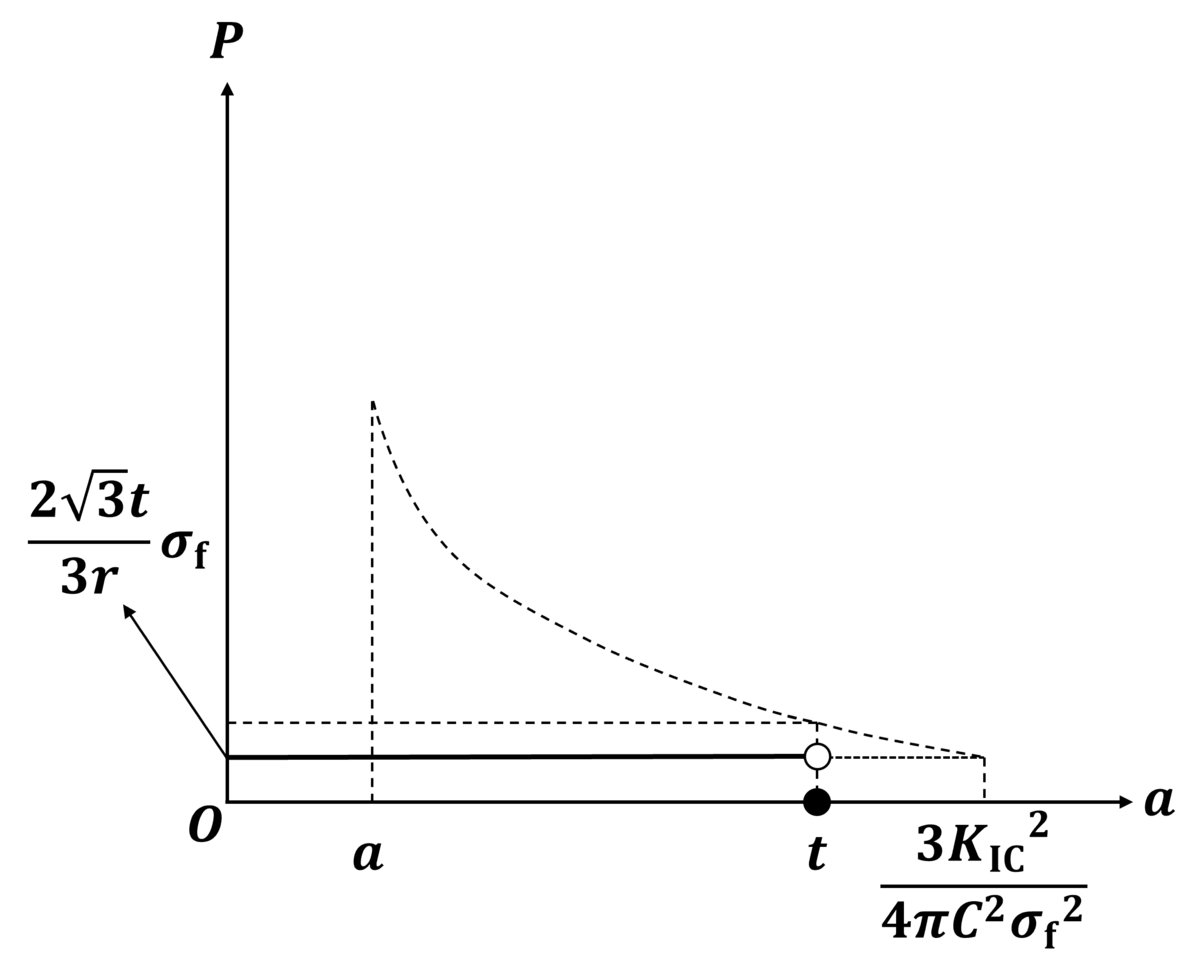
以上をまとめると破壊が生じる内圧とき裂長さaとの関係は下図のようになります。
以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |

