今回は東大院機械工学専攻2023年熱力学IIを解説したいと思います。
ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。
なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。
問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。
問題を解くのに必要な知識
・熱エネルギーバランス
・フーリエの法則
解答本文
いつもとは違い相変化を伴う伝熱です。ですが結局のところ熱エネルギーバランスを考えるというのはそこまで変わらないので焦らず解いていきましょう。
ちなみにH16年に容器の水が底から凍っていくという類題が出ています。
あまりH19より前の問題は解説をする気はないんですが、伝熱に関してはあまり熱エネルギーバランスを演習する問題集とかがなく、演習量が不足しがちなのでこんな感じで遡って解説していきたいなと思ってます。
(1)固相AおよびBにおける熱流束を答える問題
固相A内では温度勾配が0なのでフーリエの法則から
固相B内の温度勾配は
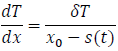
なので、フーリエの法則から熱流束は
となります。qB(t)は左向きなので－がつくわけですね。
(2)s(t)における熱収支を表す式を求める問題
下図のように微小時間dt間に界面がds(t)だけ移動したとします。ただし、ds(t)<0です。
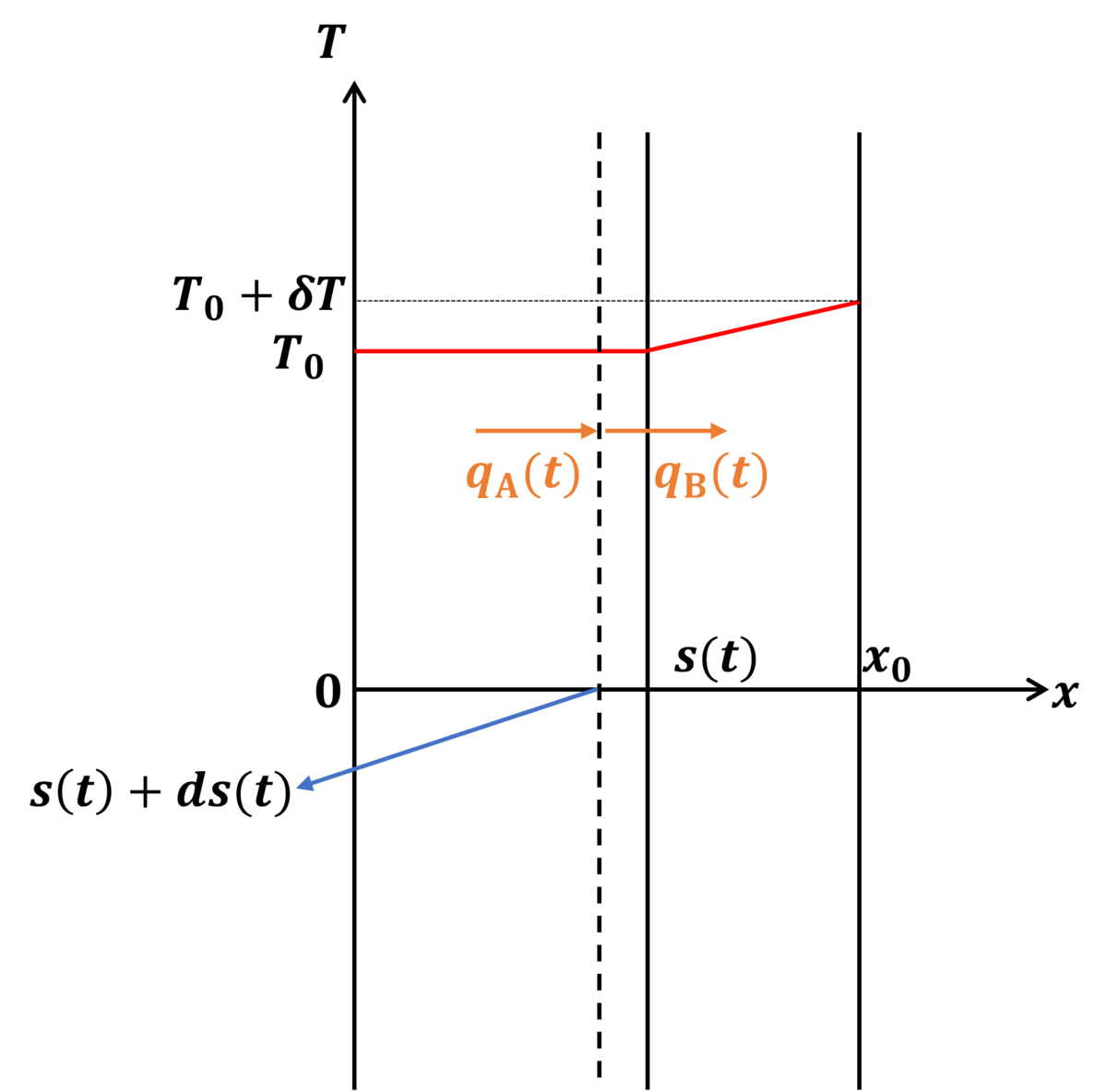
この相変化による熱量変化dQ1は単位面積あたり
ただし、ここで相変化における熱量変化はプラスになることから、マイナスがつくことに注意してください。ds(t)<0なのでマイナスを付けないとdQ1がマイナスになってしまいます。界面から固相Aへの伝熱量qA(t)および固相Bから界面への伝熱量qB(t)は問い(1)から
微小時間dt間における界面の熱バランス式は
(相変化によるの熱量の変化)＝(熱移動による熱量の変化)
となるので
これに上の式を代入して整理すると
が得られます。
(3)s(t)を求める問題
t=0のときs(t)=(x0)^2なのでC1は
これを式(Ⅱ)に代入すると
という2次方程式が得られます。これから
が得られますが、ここでs(t)は時間が経過すると小さくなっていく、つまり
をみたすのでs(t)は
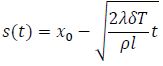
となります。
(4)x=0を除く平板全体が固相Bになる時刻を求める問題
s(t)=0としてtを求めれば
となります。
以上で解説は終わりです。最後まで読んでくれてありがとうございました。
人気ブログランキング |
にほんブログ村 |
