【院試解答】京大院機械理工学専攻H27流体力学1

どうもSNです。今回は京大院機械理工学専攻平成27年流体力学の1を解説したいと思います。

ガバガバなところがあったり間違っているかもしれませんが解答の参考にしてください。

なお問題をそのまま載せるのは権利の都合上まずいと思うので載せません。

問題が欲しいという方はコメントするかtoriatama321@gmail.comに連絡してください。

問題を解くのに必要な知識

・連続の式

・ナビエ・ストークス方程式

解答本文

ナビエ・ストークス方程式を導出したりやることが多い問題です。完答するのはかなり苦労する問題だと思うので、できるところをしっかり正確に解きましょう。

1-1.連続の式を書く問題

水の密度は一定なので連続の式は

と書けます。

1-2.(1)辺Aから流入する質量を求める問題

辺Aから流入する水の質量は

となります。

1-2.(2)辺Aから流入するx方向の運動量を求める問題

辺Aから流入する水が持つx方向の運動量は

となります。

1-2.(3)辺A、Cから流入するx方向の運動量の合計を求める問題

辺Cから流入する水が持つx方向の運動量は

なので辺A、Cから流入する水が持つx方向の運動量の合計は

となります。ここで点Pにおける流速を添え字なしのu,vとおくとΔは微小なので

が成立します。これらを先ほどの式に代入し、3次以上の微小項を無視すれば運動量の合計は

と求まります。

1-2.(4)圧力が辺A、Cを通して与えるx方向の運動量の合計を求める問題

圧力が辺A、Cを通して領域内の水に与えるx方向の運動量の合計は

となります。ここで点Pにおける圧力をpとおくとΔは微小なので

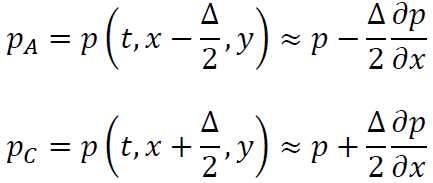
が成立します。これらを先ほどの式に代入すると求める運動量の合計は

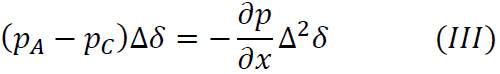
と表されます。

1-2.(5)式(1.1)を導出する問題

辺Ｂから流入する水が持つx方向の運動量は

辺Dから流入する水が持つx方向の運動量は

以上より辺B、Dから流入する水が持つx方向の運動量は

となります。ここでΔは微小なので

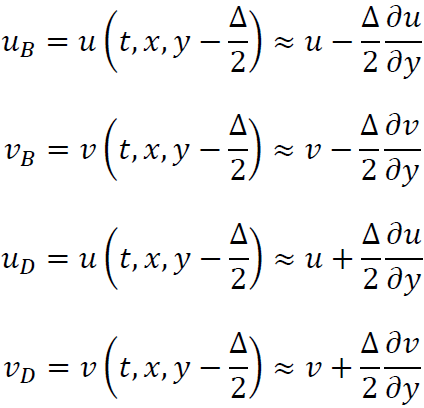
これらを先ほどの式に代入し、3次以上の微小項を無視すれば辺B、Dから流入する水が持つx方向の運動量の合計は

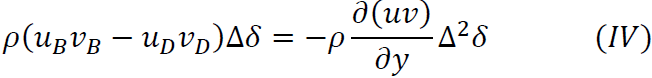
となります。

また、微小時間δ間の流体の運動量変化は

ここでδは微小なので

これを先ほどの式に代入すると微小時間δ間の流体の運動量変化は

これが式(Ⅱ)～(IV)の合計に等しくなるので

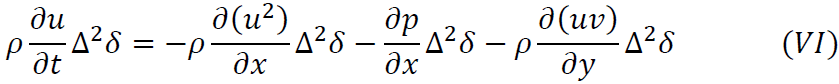
ここで

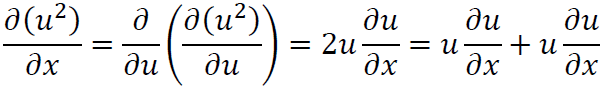
なので式(VI)は

ここで括弧内は式(I)より0なので式(1.1)と同様の式が導かれます。

1-3.(1)式(1.1)、(1.2)の対流項が無視できる条件を求める問題

連続の式の各項のオーダーは

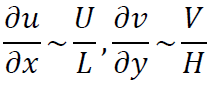
と表せます。これらのオーダーは同程度でなければならないのでVのオーダーは

となります。これを用いると式(1.1)の各項のオーダーは

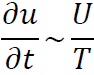
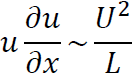
以上からx方向の対流項が無視できるための条件は

同様に式(1.2)の各項のオーダーは

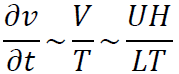
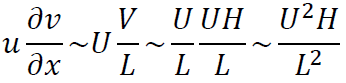
以上からy方向の対流項が無視できるための条件は

式(VII)、(VIII)をまとめると対流項を無視できるための条件は

と求まります。

1-3.(2)対流項を無視できるための条件の物理的意味を答える問題

前の問いで求めた条件の右辺のL/T及びH/Tは波の速度成分なので条件の物理的意味は

それぞれの方向の波の進行速度が対応する流体の流速成分と比較して十分に大きいこと。

と書けます。

1-4.(1)流速vをU(y)、k、ωを用いて表す問題

連続の式より

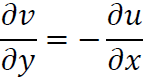
ここで

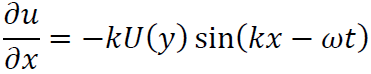
なのでこれを連続の式に代入すると

これの両辺をyで積分するとvは

と求まります。

1-4.(2)Ωが時間的に変化しないことを示す問題

Ωを時間で微分すると

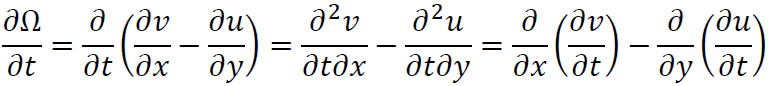
となります。ここで式(1.1)及び(1.2)の対流項を無視した時の形は

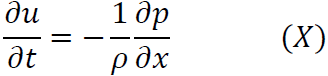
なのでこれらより

なのでΩを時間で微分した式に代入すれば

となります。よって問1-3の仮定の下ではΩは時間的に変化しないことが示せます。

1-4.(3)問い(1)、(2)を用いて流速vを求める問題

Ωの時間微分の際に出てきた

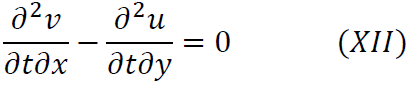
を元に考えていきます。各項を計算すると

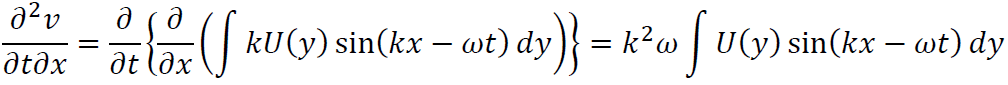
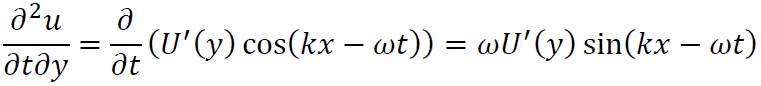
となるのでこれを式(XII)に代入すれば

となります。この両辺をyで微分して整理すると

これがtに関係なく成立するとき

が成立する必要があります。これを積分定数をC1、C2として解くと

これを式(IX)に代入するとvは

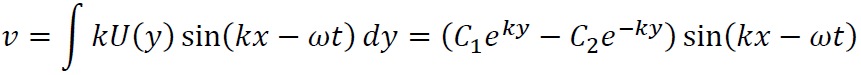
となります。ここでy=0でv=0なのでC1=C2がわかり、

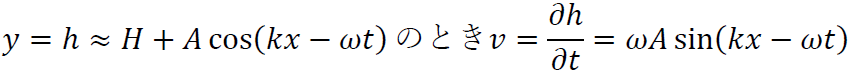
から

がわかるのでこれよりvは

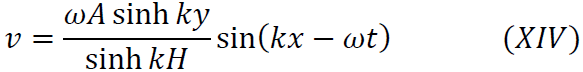
と求まります。

1-4.(4)ω^2=kgtanhkHの関係が成立することを示す問題

式(XIV)より

これを式(XI)に代入すると

が成立します。任意関数をC(x,t)として両辺をyで積分するとpは

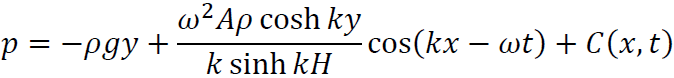
ここで境界条件の

を適用すると

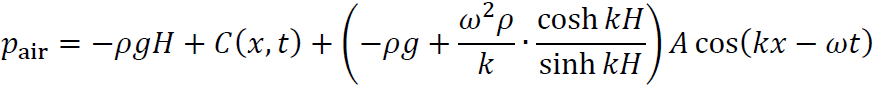
が成立します。これが成り立つためには

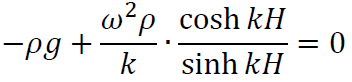
の2つが成立する必要があります。よって

の関係が導出できました。

以上で今回の記事は終わりです。最後まで読んでくれてありがとうございました。

人気ブログランキング

にほんブログ村